Hidup Smart: MATERI MATEMATIKA KELAS 7 SMP/MTSn BAB 8 : SEGITIGA DAN SEGI EMPAT

SEGITIGA

Pengertian Segitiga

Jika tiga buah titik A, B dan C yang tidak segaris saling di hubungkan,dimana titik A dihubungkan dengan B, titik B dihubungkan dengan titik C, dan titik C dihubungkan dengan titik A. Sehingga menghasilkan tiga buah ruas garis yang membentuk sebuah bangun yang disebut segitiga. Jadi segitiga merupakan bentuk bangun datar yang dibatasi oleh tiga ruas garis.

Sisi segitiga ABC diatas adalah AB, BC dan AC. Sedangkan ∠ BAC, ∠ ABC, dan ∠ ACB disebut sudut segitiga ABC. Besar jumlah ketiga sudut tersebut adalah adalah $180^{0}$ .

Jenis-jenis Segitiga

Berdasarkan panjang sisinya segitiga dibedakan menjadi:

1. Segitiga Sama kaki

Segitiga Sama kaki merupakan sebuah segitiga yang memiliki dua sisi yang sama panjang dan sudut-sudut alasnya yang sama besar. Perhatikan gambar segitiga berikut:

Pada gambar segitiga di atas AC = BC, dan kedua sudut alasanya sama besar yaitu ∠ BAC dan ∠ ABC. Adapun sifat-sifat segitiga sama kaki adalah:

a. dapat dibentuk dari dua buah segitiga siku-siku yang kongruen;

b. mempunyai dua buah sisi yang sama panjang dan dua buah sudut yang sama besar;

c. mempunyai satu sumbu simetri dan dapat menempati bingkainya dengan tepat dalam dua cara.

2. Segitiga Sama Sisi

Segitiga sama sisi merupakan sebuah bangun segitiga yang memiliki ukuran panjang sisi-sisinya sama panjang dan semua sudut-sudutnya sama besar. Perhatikan gambar segitiga berikut:

Pada gambar segitiga di atas AB = BC = AC,dan ∠ ABC = ∠ ACB = ∠ BAC =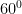 $60^{0}$ . Adapun sifat-sifat segitiga sama sisi adalah:

a. mempunyai tiga buah sisi yang sama panjang;

b. mempunyai tiga buah sudut yang sama besar (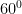 $60^{0}$ ) dan jumlah ketiga sudutnya adalah $180^{0}$ .

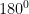c. mempunyai tiga buah sumbu simetri dan dapat menempati bingkainya dengan tepat dalam enam cara.

3. Segitiga Sembarang

Segitiga sembarang merupakan suatu bangun segitiga yang ketiga ukuran panjang sisi-sisinya berbeda atau tidak sama.

Pada gambar segitiga di atas sisi AB ≠ BC ≠ AC, dan ∠ ABC ≠ ∠ ACB ≠ ∠ BAC.

Berdasarkan besar sudutnya segitiga dibedakan menjadi

1. Segitiga siku-siku

Segitiga siku-siku adalah segitiga yang salah satu sudutnya siku-siku yaitu 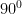$90^{0}$ . Perhatikan gambar segitiga berikut:

Pada gambar di atas ∠BAC adalah sudut siku-siku yaitu $90^{0}$ .

2. Segitiga lancip

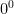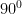Segitiga lancip adalah segitiga yang semua sudutnya lancip yaitu sudut yang besarnya di antara $0^{0}$ dan $90^{0}$ . Perhatikan gambar segitiga berikut:

Pada gambar di atas ∠ABC, ∠ABC, ∠ABC semuanya adalah sudut lancip.

3. Segitiga tumpul

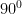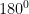Segitiga tumpul adalah segitiga yang salah satu sudutnya tumpul yaitu sudut diantara $90^{0}$ dan $180^{0}$ . Perlu ditegaskan di sini bahwa hanya satu sudut saja yang tumpul.

Pada gambar di atas ∠ ABC adalah sudut tumpul.

Menghitung Keliling dan Luas Segitiga

1. Keliling Segitiga adalah jumlah panjang ketiga sisinya.

K = jumlah dari ketiga sisinya

K = a + b + c

2. Luas segitiga

$L\; =\; \frac{1}{2}\times alas\times tinggi$

Sekian dulu pembahasan kali ini tentang mengenal bangun ruang segitiga. Semoga dapat menambah pengetahuan kita semua. Pembahasan tentang materi segitiga akan dibahas pada materi matematika selanjutnya.

SEGI EMPAT

PERSEGI

Persegi adalah Bangun segi empat yang keempat sisinya sama panjang (AB=BC=CD=AD), dan keempat sudutnya siku-siku.

Sifat-sifat :

1. Semua sisinya sama

panjang

2. Sudut-sudut persegi dibagi dua sama besar oleh diagonal-diagonalnya

3. Diagonal-diagonal persegi saling berpotongan tegak lurus dan merupakan sumbu simetri

PERSEGI PANJANG

Persegi panjang adalah Bangun segi empat yang memiliki dua pasang sisi sejajar dan sama panjang serta memiliki empat sudut siku-siku

Sifat-sifat :

1. Sisi-sisi yang berhadapan sama

panjang dan sejajar

2. Sudut-sudut persegi panjang sama besar dan merupakan sudut siku-siku

3. Diagonal-diagonal sama panjang dan saling membagi dua sama panjang

JAJAR GENJANG

Jajar genjang dapat di bentuk dari segitiga dan bayangannya setelah di putar 180⁰ dengan pusat titik tengah salah satu sisi segitiga

Sifat-sifat :

1. Sisi-sisi yang berhadapan sama

panjang dan sejajar

2. Sudut-sudut yang berhadapan sama besar

3. Jumlah dua sudut yang berdekatan adalah 180⁰

4. Diagonal-diagonalnya saling membagi dua sama panjang

BELAH KETUPAT

Belah ketupat dapat dibentuk dari segitiga sama kaki dan bayangannya oleh pencerminan terhadap alas segitiga sama kaki tersebut

Sifat-sifat Belah ketupat :

1. Sisi-sisinya sama panjang

2. Kedua digonalnya merupakan sumbu simetri dan membagi dua sama besar

3. Sudut – sudut yang berhadapan sama besar dan terbagi menjadi dua sama besar oleh diagonalnya

4. Kedua diagonal berpotongan tegak lurus

5. Kedua diagonalnya saling membagi dua sama panjang

LAYANG-LAYANG

Layang-layang dapat di bentuk dari dua segitiga samakaki yang alasnya sama panjang dan berimpit

Sifat-sifat Layang-layang :

1. Memiliki dua pasang sisi sama panjang

2. Sepasang sudut yang berhadapan sama besar

3. Salah satu diagonalnya merupakan sumbu simetri

4. Salah satu diagonalnya membagi diagonal lainnya menjadi dua bagian sama panjang dan kedua diagonal itu saling tegak lurus

TRAPESIUM

Trapesium adalah Bangun segi empat yang memiliki tepat sepasang sisi yang berhadapan sejajar

Berikut ini ada delapan contoh soal mengenai segitiga kongruen. Semoga bermanfaat.

Perhatikan gambar berikut ini
1. Buktikan bahwa $\Delta ABC$ dan $\Delta EBF$ kongruen !
2. Sebutkan pasangan sudut yang sama besar !
Tutup Jawaban
1. Perhatikan $\Delta ABC$ dan $\Delta EBF$
  $\begin{align*} AC &= EF \\ AB &= EB \\ \angle ABC &= \angle EBF (=90^{\circ}) \end{align*}$
  Jadi $\Delta ABC$ dan $\Delta EBF$ kongruen (sisi, sisi, sudut).
2. Pasangan sudut yang sama besar adalah :
  $\begin{align*} \angle ABC &= \angle EBF = 90^{\circ} \\ \angle CAB &= \angle FEB \\ \angle ACB &= \angle EFB \end{align*}$
Berikut ini adalah gambar dua segitiga

Apakah kedua segitiga tersebut kongruen ? Buktikan !

Tutup Jawaban

Perhatikan $\Delta PQR$ dan $\Delta XYZ$
$\begin{align*} PQ &= YX \\ \angle Y &= 180^{\circ} - 30^{\circ} - 30^{\circ} \\ &= 120^{\circ} \\ \angle P &= \angle Y \\ PR &= YZ \end{align*}$
Jadi, $\Delta PQR$ dan $\Delta XYZ$ kongruen karena mempunyai dua sisi yang sama, yaitu $PQ=YX$ dan $PR=YZ$ , serta 1 sudut yang sama yaitu $\angle P = \angle Y$ (sisi, sudut, sisi)
Lihatlah gambar di bawah ini !

Apakah kedua segitiga di atas kongruen ? Buktikan !

Tutup Jawaban

Lihat $\Delta MKL$ dan $\Delta TRS$
$\begin{align*} \angle K &= \angle R \\ \angle L &= \angle S \\ \angle M &= \angle T \\ KL &\neq RS \end{align*}$
Walaupun ketiga sudut kedua segitiga tersebut sama, tetapi tidak menjamin kedua segitiga tersebut kongruen. Oleh karena itu kita perlu memeriksa minimal 1 sisi yang bersesuaian, yaitu sisi KL dengan RS. Ternyata panjang $KL \neq RS$ sehingga bisa disimpulkan bahwa kedua segitiga tersebut TIDAK kongruen.
Coba perhatikan gambar di bawah ini !

$\angle BAD = \angle ABC$ dan $BC=AD$ . Buktikan bahwa $\Delta DAB$ dan $\Delta CAB$ kongruen !

Tutup Jawaban

Pisahkan bangun diatas dan putar agar menjadi dua segitiga yang terlihat sebangun, yaitu $\Delta DAB$ dan $\Delta CBA$

Perhatikan $\Delta DAB$ dan $\Delta CBA$
$\begin{align*} DA &= CB \\ \angle DAB &= \angle CBA \\ AB &= BA (berhimpit) \end{align*}$
Jadi $\Delta DAB$ dan $\Delta CBA$ kongruen (sisi, sudut, sisi).
Perhatikan gambar berikut !

Buktikan bahwa $\Delta ADC$ dan $\Delta DBC$ kongruen !

Tutup Jawaban

Perhatikan $\Delta ADC$ dan $\Delta DBC$
$\begin{align*} AD &= DB \\ AC &= BC \\ DC &= DC \end{align*}$
Jadi kedua segitiga tersebut adalah kongruen karena ketiga sisinya sama panjang (sisi, sisi, sisi).
Periksa apakah $\Delta AEC$ dan $\Delta DEB$ dibawah ini kongruen !

Lihat Jawaban
Pada gambar berikut ini, panjang PR = 12 cm dan QR = 10 cm.
1. Buktikan bahwa $\Delta ABC$ dan $\Delta PQR$ adalah kongruen !
2. Tentukan Panjang AC !
Tutup Jawaban
1. Cari $\angle P$ dahulu
  $\begin{align*} \angle P &= 180^{\circ} - 65^{\circ} - 70^{\circ} \\ &= 45^{\circ} \end{align*}$
  Setelah itu, putar $\Delta PQR$ agar sudutnya bersesuaian seperti gambar di bawah ini
  
  $\begin{align*} \angle A &= \angle P \\ AB &= PQ \text{(diketahui)} \\ \angle B &= \angle Q \end{align*}$
  Jadi $\Delta ABC$ kongruen dengan $\Delta PQR$ (sudut, sisi, sudut)
2. Panjang AC adalah sama dengan panjang PR, yaitu 12 cm.
Lihatlah gambar di bawah ini.

Pada gambar di atas, QR = QS, PQ = QT. Buktikan bahwa :
1. $\Delta PQR$ dan $\Delta TQS$ kongruen !
2. $\Delta PSU$ dan $\Delta TRU$ kongruen !
Tutup Jawaban
1. Pisahkan $\Delta PQR$ dan $\Delta TQS$ seperti gambar di bawah
  $\begin{align*} QR &= QS \text{ (diketahui)}\\ PQ &= QT \text{ (diketahui)} \\ \angle P &= \angle T \end{align*}$
  Jadi, kedua segitiga tersebut kongruen (sisi, sisi, sudut).
2. Perhatikan potongan $\Delta PSU$ dan $\Delta TRU$ berikut:
  
  Perhatikan bahwa
  $\begin{align*} &SP = QS - PQ \\ &RT = QR - QT \\ &\text{sedangkan} \\ &QR = QS \text{ (diketahui)}\\ &PQ = QT \text{ (diketahui)}\\ &\text{dapat disimpulkan bahwa } \\ &SP = RT \end{align*}$
  Selanjutnya periksa sudut-sudutnya
  $\begin{align*} \angle SUP &= \angle TUR \\ \angle UPS &= \angle RTU \\ \end{align*}$
  Jadi, $\Delta PSU$ dan $\Delta TRU$ adalah kongruen (sisi, sudut, sudut)
Soal Prediksi Segiempat.
1. Panjang diagonal - diagonal persegi panjang adalah (7x - 8) cm dan (4x + 7) cm.
Tentukan Panjang diagonal persegi panjang tersebut.
ans : panjang diagonal persegi panjang adalah sama.

2. Keliling sebuah persegi panjang 60 cm. Sedangkan panjang : lebar = 3 : 2.
Tentukan ukuran persegi panjang.

ans : k = 2(p+l), dengan p = 3x dan l = 2x.
L = p.l

3. Keliling persegi panjang 44 cm, Sedangkan panjangnya 12 cm. Tentukan luas persegi panjang.

ans : l = (k:2)- p, maka L = p.l

4. Diagonal - diagonal persegi PQRS berpotongan di titik O. Jika besar sudut POQ = 5y,
Tentukan nilai y.

ans : diagonal-diagonal persegi sama panjang, saling tegak lurus dan saling membagi 2 sama panjang.

5. Luas suatu persegi 16 a pangkat 2 cm persegi. Tentukan keliling persegi yang ddinyatakan
dengan a.

ans:
L = s pangkat 2, maka s = akar pangkat 2 dari 16 a kuadrat, jd s = 4a, k = 4.s=4.4a= 16a

6. Pada jajargenjang ABCD, panjang AD = (3x - 4) cm dan BC = (x + 10) cm.
Tentukan panjang AD.
ans : sisi-sisi yang berhadapan sama dan sejajar.
7. Pada jajargenjang PQRS, sudut P : sudut Q = 2 : 3. Tentukan besar sudut P dan sudut Q.

ans : sudut-sudut yang berdekatan adalah sepihak dan berjumlah 180 derajat

8. Diketahui jajargenjang ABCD dengan panjang AD = 8 cm, CD = 10 cm dan
garis tinggi DE = 7 cm. Tentukan luas jajrgenjang ABCD.

ans : L = a.t

9. Pada jajagenjang PQRS, panjang PQ = 15 cm, PS = 10 cm, dan garis tinggi TR = 8 cm.
Tentukan panjang garis tinggi RU.

ans : L = a.t dan L = a1.t1 =a2.t2,

10. Pada jajargenjang KLMN, besar sudut K = (x + 5) dan sudut N = (3x - 25).
Tentukan besar sudut L.

ans : sudut-sudut yang berhadapan sama besar
11. Panjang alas dan tinggi suatu jajargenjang berbanding sebagai 3 : 2.
Jika luas jajargenjang tersebut 150 cm persegi. Tentukan panjang alasnya.
ans : L = a.t, L = 3x. 2x = 150, a = 3x dan t = 2x