Bentuk-bentuk aljabar
Persamaan dan pertidaksamaan linear
- Persamaan Linear Satu Variabel
Contoh :
r:101. r + 3 = 10.
r + 3 - 3 = 10 - 3 (sama sama dikurangi dengan bilangan yang sama yaitu 3) r = 72. 3p = 12
3p / 3 = 12/3 (sama-sama dibagi dengan bilangan yang sama yaitu 3) p = 4
- Pertidaksamaan Linear satu variabel
- Ruas Kiri dan kanan dapat ditambah, dikurangi, dikali, atau dibagi bilangan yang sama
- jika variabel bertanda minus, harus diganti menjadi positif dengan mengali bilangan negatif dan membalikan tanda
5v - 7 + 7 > 23 + 7 5v / 5 > 30 / 5 v > 62. -2a < 10
-2a / -2 > 10 / -2 a > -5\3. -2a < 10
-2a / -2 > 10 / -2 a > -5\
Contoh 1. Tentukan hasil penjumlahan 5p – 4q + 8 dan 7p + 9q -10
Jawab : suku yang sejenis adalah 5p dan 7p, -4q dan 9q, 8 dan -10
Maka, 5p – 4q + 8 + 7p + 9q – 10 = (5p + 7p) + (-4q + 9q) + (8 + (-10))
= 12p + 5q + (-2)
= 12p + 5q – 2
Contoh 2. Tentukan hasil pengurangan 8x2 – 6x dari 15x2 – 2x
Jawab : suku yang sejenis adalah 8x2 dan 15x2, -6x dan -2x
Maka, 15x2 – 2x – 8x2 – 6x = (15x2 – 2x) – (8x2 – 6x)
= 15x2 – 2x – 8x2 + 6x
= 15x2 – 8x2 – 2x + 6x
= 7x2 + 4x
2. Perkalian suku dua
Perkalian pada suku dua dapat dilakukan dengan menggunakan sifat distributif.
Contoh 1. (3x – 5) (x + 7) = 3x (x + 7) -5(x + 7)
= 3x2 + 21x -5x -35
= 3x2 + 16x – 35
Contoh 2. (4p + q) (2p – 8q) = 4p (2p – 8q) + q (2p – 8q)
= 8p2 – 32pq + 2pq – 8q2
= 8p2 – 30pq – 8q2
3. Pemfaktoran
Beberapa macam bentuk pemfaktoran antara lain adalah :
- ax + ay = a (x + y)
- x2 – 2xy + y2 = (x – y) (x – y)
- x2 – y2 = (x + y) (x – y)
- x2 + 10x + 21 = (x + 7) (x + 3)
- 3x2 – 4x – 4 = (3x + 2) (x -2)
Contoh 2. x2 – 7x 18 = (x + 2) (x – 9)
4. Pecahan dalam Bentuk Aljabar
Perlu diingat bahwa pada suatu pecahan, termasuk pecahan bentuk aljabar, penyebut dari pecahan itu tidak boleh 0 (nol). Untuk melakukan operasi penjumlahan dan pengurangan pecahan, jika penyebut dari masing-masing pecahan tidak sama, maka penyebut dari pecahan itu harus disamakan.
Contoh 1.
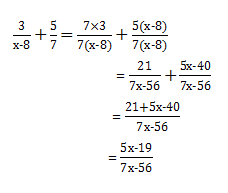
Contoh 2.

Beberapa contoh soal yang berkaitan dengan Operasi Bentuk Aljabar
3. Hasil dari (3x – 2) (4x – 5) = …..
4. Pemfaktoran dari 49a2 – 25b2 = …..
5. Bentuk sederhana dari
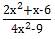

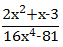
Tidak ada komentar:
Posting Komentar